Вычисление криволинейного интеграла первого рода. Плоский случай

Если кривая лежит на какой-либо координатной плоскости, например, плоскости $\mathbf { \textit { Оху } } $, и задаётся функцией $y=y(x),\;a\leqslant x\leqslant b$, то, рассматривая $\mathbf { \textit { х } } $ как параметр, получаем следующую формулу для вычисления интеграла: $\int\limits_L { f(x,y)dl=\int\limits_a^b { f(x,y(x))\sqrt { 1+[ { y } '(x)]^2 } \,dx } } $. Аналогично, если кривая задаётся уравнением $x=x(y),\;c\leqslant y\leqslant d$, то $\int\limits_L { f(x,y)dl=\int\limits_c^d { f(x(y),y)\sqrt { 1+[ { x } '(y)]^2 } \,dy } } $.

Примеры:

Пример 1

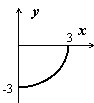
Вычислить $\int\limits_L { xy^2dl } $, где $L$ - четверть окружности $x^2+y^2=9$, лежащая в четвёртом квадранте.

Решение:

1. Рассматривая $\mathbf { \textit { х } } $ как параметр, получаем $y=-\sqrt { 9-x^2 } ,\; { y } '(x)=\frac { x } { \sqrt { 9-x^2 } } , \quad \sqrt { 1+ { y } '^2(x) } =\frac { 3 } { \sqrt { 9-x^2 } } $, поэтому $\int\limits_L { xy^2dl } =\int\limits_0^3 { x\left[ { -\sqrt { 9-x^2 } }\right]^2\cdot \frac { 3 } { \sqrt { 9-x^2 } } } dx= 3\int\limits_0^3 { x\cdot \sqrt { 9-x^2 } } dx=-\left. { \left[ { \sqrt { 9-x^2 } }\right]^3 }\right|_0^3 =27$
2. Если за параметр взять переменную $\mathbf { \textit { у } } $, то $x=\sqrt { 9-y^2 } ,\; { x } '(y)=\frac { -y } { \sqrt { 9-y^2 } } , \quad dl=\frac { 3dy } { \sqrt { 9-y^2 } } $ и $\int\limits_L { xy^2dl } =\int\limits_0^3 { \sqrt { 9-y^2 } y^2\cdot \frac { 3 } { \sqrt { 9-y^2 } } } dy=\left. { y^3 }\right|_0^3 =27$
3. Естественно, можно взять обычные параметрические уравнения окружности $x=3\cos t, \quad y=3\sin t,\;3\pi /2\leqslant t\leqslant 2\pi : \int\limits_L { xy^2dl } =\int\limits_ { 3\pi /2 } ^ { 2\pi } { 3\cos t\cdot (3\sin t)^2\cdot \sqrt { (-3\sin t)^2+(3\cos t)^2 } } dy=81\left. { \frac { \sin t } { 3 } ^3 }\right|_ { 3\pi /2 } ^ { 2\pi } =27$

Если кривая задана в полярных координатах $r=r(\varphi ),\;\varphi _0 \leqslant \varphi \leqslant \varphi _k $, то $dl=\sqrt { r^2(\varphi )+ { r } '^2(\varphi ) } d\varphi $, и $\int\limits_L { f(x,y)dl } =\int\limits_ { \varphi _0 } ^ { \varphi _k } { f(r(\varphi )\cos \varphi ,r(\varphi )\sin \varphi )\cdot \sqrt { r^2(\varphi )+ { r } '^2(\varphi ) } } \cdot d\varphi $.