Криволинейный интеграл. Введение

Рассмотрим следующую физическую задачу. Пусть в пространстве $\mathbf { \textit { Oxyz } } $ вдоль кривой $L=\mathop { AB } \limits^\cup $ перемещается материальная точка под воздействием силы $\mathop { F(M) } \limits^\to =P(M)\cdot \mathop i\limits^\to +Q(M)\cdot \mathop j\limits^\to +R(M)\cdot \mathop k\limits^\to $; при этом сила может меняться от точки к точке. Требуется найти работу, которая совершается силой.

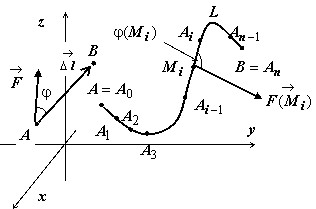
В случае, когда в качестве $L=\mathop { AB } \limits^\cup $ берётся $\mathop { \Delta l } \limits^\to \left[{ \Delta x,\Delta y,\Delta z }\right]$ - прямолинейный отрезок { левая часть рисунка } , и $\mathop { F(M) } \limits^\to =\mathop F\limits^\to \left[{ P,Q,R }\right]=const$ - постоянная сила, работа есть скалярное произведение силы на вектор перемещения точки: $A=\mathop F\limits^\to \cdot \mathop { \Delta l } \limits^\to $. Это выражение можно трактовать двумя способами.

1. По определению скалярного произведения $A=\mathop F\limits^\to \cdot \mathop { \Delta l } \limits^\to =\left( { F\cdot \cos \varphi }\right)\cdot \Delta l$. Здесь $F=\left| { \mathop F\limits^\to }\right|$, $\Delta l=\left| { \mathop { \Delta l } \limits^\to }\right|,\;\varphi $ - угол между $\mathop F\limits^\to \;\mbox { и } \;\mathop { \Delta l } \limits^\to $. Обозначим $f=F\cdot \cos \varphi $, тогда $A=f\cdot \Delta l$.
2. Если расписать скалярное произведение в координатной форме, то $A=\mathop F\limits^\to \cdot \mathop { \Delta l } \limits^\to =P\cdot \Delta x+Q\cdot \Delta y+R\cdot \Delta z$.

Пусть теперь $L$ - произвольная гладкая ограниченная кривая, и сила $\mathop { F(M) } \limits^\to $ может меняться от точки к точке { правая часть рисунка } .

Чтобы свести этот случай к предыдущему, разобьём кривую $L=\mathop { AB } \limits^\cup $ точками $A_0 =A,\;A_1 ,\;A_2 ,\ldots ,A_n =B$ на $n$ частей, на каждой из дуг $\mathop { A_ { i-1 } A_i } \limits^\cup $ выберем произвольную точку $M_i $, и, считая, что дуга $\mathop { A_ { i-1 } A_i } \limits^\cup $ - прямолинейный отрезок - вектор $\mathop { A_ { i-1 } A_i } \limits^\to \left[{ \Delta x_i ,\Delta y_i ,\Delta z_i }\right]$ длины $\Delta l_i $, и сила вдоль этого отрезка постоянна и равна $\mathop F\limits^\to (M_i )$, получим, что работа вдоль этой дуги близка к $\Delta A_i =\mathop F\limits^\to (M_i )\cdot \mathop { A_ { i-1 } A_i } \limits^\to (i=1,2,\ldots ,n)$.

Как мы видели, это выражение можно представить и в виде $\Delta A_i =\mathop F\limits^\to (M_i )\cdot \mathop { A_ { i-1 } A_i } \limits^\to =f(M_i )\cdot \Delta l_i $ { где $f(M_i )=\left| { \mathop F\limits^\to (M_i ) }\right|\cdot \cos \varphi (M_i ), \quad \;\varphi (M_i )$ - угол между $\mathop { A_ { i-1 } A_i } \limits^\to $ и $\mathop F\limits^\to (M_i )$ } , и в виде $\Delta A_i =\mathop F\limits^\to (M_i )\cdot \mathop { A_ { i-1 } A_i } \limits^\to =P(M_i )\cdot \Delta x_i +Q(M_i )\cdot \Delta y_i +R(M_i )\cdot \Delta z_i $.

Суммируя эти выражения по всем $n$ дугам, получим выражения двух интегральных сумм:

$\sum\limits_ { i=1 } ^n { f(M_i )\cdot \Delta l_i } $ и $\sum\limits_ { i=1 } ^n { P(M_i )\cdot \Delta x_i +Q(M_i )\cdot \Delta y_i +R(M_i )\cdot \Delta z_i } $.

Переход к пределу в этих интегральных суммах при $\mathop { \max } \limits_ { i=1,2,\ldots n } \Delta l_i \to 0$ приведёт к двум криволинейным интегралам:

1. $\int\limits_L { f(M)\cdot dl } $ и
2. $\int\limits_L { P(M)\cdot dx+Q(M)\cdot dy+R(M)\cdot dz } $.

Первый из этих интегралов называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги; второй - криволинейным интегралом второго рода, или криволинейным интегралом по координатам. Несмотря на то, что они описывают одну и ту же физическую величину, с математической точки зрения это разные объекты. Они имеют разные определения и разные свойства.

В частности, криволинейный интеграл первого рода не зависит от направления прохождения кривой:

$\int\limits_ { \mathop { AB } \limits^\cup } { f(M)\cdot dl } =\int\limits_ { \mathop { BA } \limits^\cup } { f(M)\cdot dl } $

{ так как угол $\phi $ между силой и кривой входит в подынтегральную функцию в явном виде } , в то время как криволинейный интеграл второго рода меняет знак при изменении направления прохождения кривой:

$\int\limits_ { \mathop { AB } \limits^\cup } { P(M)\cdot dx+Q(M)\cdot dy+R(M)\cdot dz } =-\int\limits_ { \mathop { BA } \limits^\cup } { P(M)\cdot dx+Q(M)\cdot dy+R(M)\cdot dz } $

{ вектор $\mathop { A_ { i-1 } A_i } \limits^\to \left[{ \Delta x_i ,\Delta y_i ,\Delta z_i }\right]$, координаты которого входят в интегральную сумму, меняется на вектор $\mathop { A_i A_ { i-1 } } \limits^\to \left[{ -\Delta x_i ,-\Delta y_i ,-\Delta z_i }\right]$ } .