Определение криволинейного интеграла второго рода

Пусть в пространстве $\mathbf { \textit { Oxyz } } $ дана кусочно-гладкая кривая $L=\mathop { AB } \limits^\cup $, на которой определена функция $\mathbf { \textit { P } } (\mathbf { \textit { x } } $, $\mathbf { \textit { y } } $, $\mathbf { \textit { z } } )$.

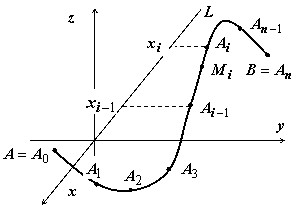
Разобьём кривую точками $\mathbf { \textit { A } } _ { 0 } (\mathbf { \textit { x } } _ { 0 } , \mathbf { \textit { y } } _ { 0 } , \mathbf { \textit { z } } _ { 0 } )=\mathbf { \textit { A } } , \mathbf { \textit { A } } _ { 1 } (\mathbf { \textit { x } } _ { 1 } , \mathbf { \textit { y } } _ { 1 } , \mathbf { \textit { z } } _ { 1 } ), \mathbf { \textit { A } } _ { 2 } (\mathbf { \textit { x } } _ { 2 } , \mathbf { \textit { y } } _ { 2 } , \mathbf { \textit { z } } _ { 2 } ), { \ldots } , \mathbf { \textit { A } } _ { i } (\mathbf { \textit { x } } _ { i } \quad \mathbf { \textit { y } } _ { i } , \mathbf { \textit { z } } _ { i } ), { \ldots } , \mathbf { \textit { A } } _ { n } (\mathbf { \textit { x } } _ { n } \quad \mathbf { \textit { y } } _ { n } , \mathbf { \textit { z } } _ { n } )=\mathbf { \textit { B } } $ на $\mathbf { \textit { n } } $ частей, на каждой из дуг $\mathop { A_ { i-1 } A_i } \limits^\cup $ выберем произвольную точку $\mathbf { \textit { M } } _ { i } (\mathbf { \textit { x } } _ { i } \quad \mathbf { \textit { y } } _ { i } $, $\mathbf { \textit { z } } _ { i } )$, найдём $\mathbf { \textit { P } } (\mathbf { \textit { M } } _ { i } )=\mathbf { \textit { P } } _ { i } (\mathbf { \textit { x } } _ { i } \quad \mathbf { \textit { y } } _ { i } $, $\mathbf { \textit { z } } _ { i } )$ и проекцию $\Delta x_i =x_i -x_ { i-1 } $ дуги $\mathop { A_ { i-1 } A_i } \limits^\cup $ на ось $\mathbf { \textit { Ох } } $ и составим интегральную сумму $\sum\limits_ { i=1 } ^n { P(M_i )\cdot \Delta x_i } $.

Если существует предел последовательности интегральных сумм при $\mathop { \max } \limits_ { i=1,2,\ldots n } \Delta l_i \to 0$, не зависящий ни от способа разбиения кривой на дуги $\mathop { A_ { i-1 } A_i } \limits^\cup (\mathbf { \textit { i } } = 1, 2, { \ldots } , \mathbf { \textit { n } } )$, ни от выбора точек $\mathbf { \textit { M } } _ { i } $, то функция $\mathbf { \textit { Р } } (\mathbf { \textit { x } } ,\mathbf { \textit { y } } ,\mathbf { \textit { z } } )$ называется интегрируемой по кривой $\mathbf { \textit { L } } $, а значение этого предела называется криволинейным интегралом второго рода, или криволинейным интегралом по координате $\mathbf { \textit { х } } $ от функции $\mathbf { \textit { Р } } (\mathbf { \textit { x } } ,\mathbf { \textit { y } } ,\mathbf { \textit { z } } )$ по кривой $\mathbf { \textit { L } } $ и обозначается $\int\limits_L { P(M)\cdot dx } $ { или $\int\limits_ { \mathop { AB } \limits^\cup } { P(M)\cdot dx } $ } .

Теорема существования

Если функция $\mathbf { \textit { Р } } (\mathbf { \textit { x } } $,$\mathbf { \textit { y } } $,$\mathbf { \textit { z } } )$ непрерывна на кривой $\mathbf { \textit { L } } $, то она интегрируема по этой кривой.

Если на кривой $\mathbf { \textit { L } } $, вместе с функцией $\mathbf { \textit { Р } } (\mathbf { \textit { x } } $,$\mathbf { \textit { y } } $,$\mathbf { \textit { z } } )$, заданы функции $\mathbf { \textit { Q } } (\mathbf { \textit { x } } $,$\mathbf { \textit { y } } $,$\mathbf { \textit { z } } )$ и $\mathbf { \textit { R } } (\mathbf { \textit { x } } $,$\mathbf { \textit { y } } $,$\mathbf { \textit { z } } )$, то, аналогично интегралу $\int\limits_L { P(M)\cdot dx } $, определяются интегралы $\int\limits_L { Q(M)\cdot dy } $ и$\int\limits_L { R(M)\cdot dz } $.

В приложениях рассматривается сумма этих интегралов, которая обозначается $\int\limits_L { P(M)\cdot dx+Q(M)\cdot dy+R(M)\cdot dz } $ и также называется криволинейным интегралом второго рода. Если кривая, по которой ведётся интегрирование, является контуром { т.е. замкнута } , то, как и для криволинейного интеграла по длине дуги, в качестве начальной { и совпадающей с ней конечной } точки можно взять любую точку кривой.