Формула Грина

Связность, односвязность, многосвязность

Напомним определения ряда понятий из теории функций нескольких переменных, которыми нам придется пользоваться.

Множество точек { на прямой, на плоскости, в пространстве } называется связным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей этому множеству.

Область { на плоскости, в пространстве } называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области.

Примеры:

Односвязны шар, параллелепипед и вообще любой выпуклый объём в пространстве. Односвязен шаровой слой, заключённый между двумя сферами. Пример неодносвязной области: тор. Все пространство односвязно и остаётся односвязным, если из него удалить точку или отрезок. Если же удалить из пространства прямую, оно потеряет свойство односвязности: окружность, охватывающую эту прямую, не удастся стянуть в точку, не пересекая прямую.

Кусочно-гладкая граница ограниченной односвязной области всегда связна, следовательно, является контуром.

Теорема Грина для односвязной области

Пусть на плоскости $\mathbf { \textit { Oxy } } $ задана односвязная область$\mathbf { \textit { D } } $, ограниченная кусочно-гладким контуром $\mathbf { \textit { C } } $. На множестве $\bar { D } =D\cup C$ определены непрерывные функции $P(x,y)$ и $Q(x,y)$, имеющие непрерывные частные производные.

Тогда $\oint\limits_С { P(x,y)dx+Q(x,y)dy=\iint\limits_D { \left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)dxdy } } $, при этом контур$\mathbf { \textit { C } } $ обходится так, что область $\mathbf { \textit { D } } $ остаётся слева.

Доказательство

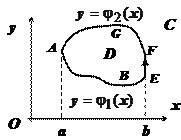
1). Пусть $\mathbf { \textit { D } } $ - простая область. Докажем сначала, что $\oint\limits_C { P(x,y)dy } =-\iint\limits_D { \frac { \partial P } { \partial y } dxdy } $.

$y=\varphi _2 (x)y=\varphi _1 (x)$

Опишем $\mathbf{\textit{D}}$ неравенствами $D:\left({\begin{array}{l} a\leqslant x\leqslant b, \\ \varphi _1 (x)\leqslant y\leqslant \varphi _2 (x). \\ \end{array}}\right.$

Тогда $-\iint\limits_D { \frac { \partial P } { \partial y } dxdy } =-\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _x (x) } { \frac { \partial P } { \partial y } dy } } =-\int\limits_a^b { \left. { P(x,y) }\right|_ { \varphi _1 (x) } ^ { \varphi _2 (x) } dx } =-\int\limits_a^b { P(x,\varphi _2 (x))dx } - +\int\limits_a^b { P(x,\varphi _1 (x))dx } = \\ =\int\limits_a^b { P(x,\varphi _1 (x))dx } -\int\limits_b^a { P(x,\varphi _2 (x))dx } =\int\limits_ { \mathop { ABE } \limits^\cup } { P(x,y)dx } + \int\limits_ { \mathop { FGA } \limits^\cup } { P(x,y)dx } $.

Если контур включает вертикальные участки, такие как $\mathbf { \textit { EF } } $, то на этих участках $\mathbf { \textit { dx } } = 0$, поэтому $\int\limits_ { \mathop { EF } \limits^\cup } { P(x,y)dx } =0$, и $y=\psi _2 (y)y=\psi _1 (y)-\iint\limits_D { \frac { \partial P } { \partial y } dxdy } =\int\limits_ { \mathop { ABE } \limits^\cup } { P(x,y)dx } +\int\limits_ { \mathop { EF } \limits^\cup } { P(x,y)dx } +\int\limits_ { \mathop { FGA } \limits^\cup } { P(x,y)dx } =\oint\limits_C { P(x,y)dx } $, что и требовалось доказать.

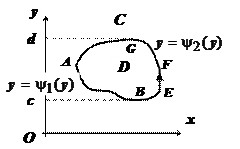
Равенство $\oint\limits_C { Q(x,y)dy } =\iint\limits_D { \frac { \partial Q } { \partial x } dxdy } $ доказывается точно также:

$\iint\limits_D { \frac { \partial Q } { \partial x } dxdy } =\int\limits_c^d { dy\int\limits_ { \psi _1 (y) } ^ { \psi _2 (y) } { \frac { \partial Q } { \partial x } dx } } =\int\limits_c^d { \left. { Q(x,y) }\right|_ { \psi _1 (y) } ^ { \psi _2 (y) } dy } = \int\limits_c^d { Q(\psi _2 (y),y)dy } -\int\limits_c^d { Q(\psi _1 (y),y)dy } = \\ = \int\limits_ { \mathop { BEFG } \limits^\cup } { Q(x,y)dy } + \int\limits_ { \mathop { GAC } \limits^\cup } { Q(x,y)dy } =\oint\limits_C { Q(x,y)dy } $.

Суммируя равенства $\oint\limits_C { P(x,y)dy } =-\iint\limits_D { \frac { \partial P } { \partial y } dxdy } $ и $\oint\limits_C { Q(x,y)dy } =\iint\limits_D { \frac { \partial Q } { \partial x } dxdy } $, получим одну из важнейших формул анализа - формулу Грина $ \oint\limits_С { P(x,y)dx+Q(x,y)dy=\iint\limits_D { \left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)dxdy } } $

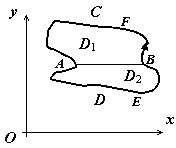
2). Пусть теперь $\mathbf { \textit { D } } $ - произвольная, не обязательно простая, область. Разобьём её на простые части. Пусть это разбиение производится отрезком $\mathbf { \textit { АВ } } $ и пусть подобласти $\mathbf { \textit { D } } _ { 1 } $ и $\mathbf { \textit { D } } _ { 2 } $ - результат разбиения. Для этих подобластей формула Грина доказана:

$\oint\limits_ { ABFA } { Pdx+Qdy=\iint\limits_ { D_1 } { \left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)dxdy } } $ и $\oint\limits_ { AEBA } { Pdx+Qdy=\iint\limits_ { D_2 } { \left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)dxdy } } $.

По свойству аддитивности $\oint\limits_ { ABFA } { Pdx+Qdy } =\oint\limits_ { AB } { Pdx+Qdy } +\oint\limits_ { BFA } { Pdx+Qdy } $, $\oint\limits_ { AEBA } { Pdx+Qdy } =\oint\limits_ { AEB } { Pdx+Qdy } +\oint\limits_ { BA } { Pdx+Qdy } = \oint\limits_ { AEB } { Pdx+Qdy } -\oint\limits_ { AB } { Pdx+Qdy } $

Суммируя эти выражения, убеждаемся, что криволинейные интегралы по отрезкам $\mathbf { \textit { АВ } } $ и $\mathbf { \textit { ВА } } $ взаимно уничтожаются, а сумма интегралов по кривым $\mathbf { \textit { BFA } } $ и $\mathbf { \textit { AEB } } $ даёт интеграл по контуру $\mathbf { \textit { C } } $, т.е. формула Грина верна и для области, не являющейся простой.

Доказательство остаётся справедливым и в случае, когда разбиение производится добавлением большего числа, чем одна, кривых.

Теорема Грина для многосвязной области

Пусть теперь $\mathbf { \textit { D } } $ многосвязная на плоскости $\mathbf { \textit { Oxy } } $. Граница многосвязной области состоит из нескольких связных частей, не имеющих общих точек.

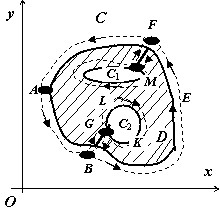
Рассмотрим случай, когда граница области $\mathbf { \textit { D } } $ { на рисунке область заштрихована } состоит из внешнего контура $\mathbf { \textit { C } } $ и внутренних контуров $\mathbf { \textit { C } } _ { 1 } $ и $\mathbf { \textit { C } } _ { 2 } $.

Соединим контур $\mathbf { \textit { C } } $разрезом $\mathbf { \textit { FM } } $ с контуром $\mathbf { \textit { C } } _ { 1 } $, разрезом $\mathbf { \textit { BG } } $ - с контуром $\mathbf { \textit { C } } _ { 2 } $. { Под словами "соединим разрезом $\mathbf { \textit { BG } } $ " подразумевается то, что мы удалим из $\mathbf { \textit { D } } $ отрезок $\mathbf { \textit { BG } } )$.

Область $ { D } '=D\backslash (BG\cup FM)$ с границей $ { \Gamma } '=\mathop { AB } \limits^\cup \cup BG\cup (C_2 =\mathop { GLKG } \limits^\cup )\cup GB\cup \mathop { BF } \limits^\cup \cup FM\cup C_1 \cup MF\cup \mathop { MA } \limits^\cup $ односвязна, поэтому для неё справедлива формула Грина:

$\oint\limits_ { { \Gamma } ' } { Pdx+Qdy=\iint\limits_ { { D } ' } { \left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)dxdy } } $

Двойные интегралы по областям $\mathbf { \textit { D } } $ и $ { D } '\mathbf { } $ равны { площадь разрезов равна нулю } ; в криволинейный интеграл по кусочно-гладкой кривой $ { \Gamma } '$ интегралы по разрезам входят с противоположными знаками { $\int\limits_ { BG } { Pdx } +Qdy$ и $\int\limits_ { GB } { Pdx } +Qdy$, например } и поэтому взаимно уничтожаются, поэтому оказывается справедлива теорема Грина для многосвязной области :

пусть на плоскости $\mathbf { \textit { Oxy } } $ дана многосвязная область$\mathbf { \textit { D } } $ с границей $\Gamma $. На множестве $\bar { D } =D\cup \Gamma $ определены непрерывные функции $P(x,y)$ и $Q(x,y)$, имеющие непрерывные частные производные. Тогда $\oint\limits_\Gamma { P(x,y)dx+Q(x,y)dy=\iint\limits_D { \left( { \frac { \partial Q } { \partial x } -\frac { \partial P } { \partial y } }\right)dxdy } } $, при этом каждая часть полной границы $\Gamma $ обходится так, что область $\mathbf { \textit { D } } $ остаётся слева.