Вычисление двойного интеграла. Двукратный { повторный } интеграл

Определение простой { правильной } области

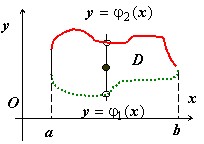
Область $ \mathbf { \textit { D } } $ на плоскости $\mathbf { \textit { Oxy } } $будем называть $\textbf { простой { правильной } в направлении оси } \quad \mathbf { \textit { Oy } } $, если любая прямая, проходящая через внутреннюю точку области $\mathbf { \textit { D } } $ и параллельная оси $\mathbf { \textit { Oy } } $, пересекает границу $\mathbf { \textit { D } } $ в двух точках.

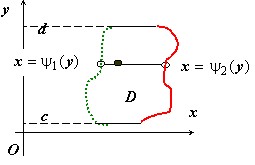
Аналогично определяется область, $\textbf { простая { правильная } в направлении оси } \mathbf { \textit { Ox } } $: любая прямая, проходящая через внутреннюю точку области $\mathbf { \textit { D } } $ и параллельная оси $\mathbf { \textit { Oх } } $, пересекает границу $\mathbf { \textit { D } } $ в двух точках.

Область, правильную { простую } в направлении обеих осей, будем называть $\textbf { правильной } $.

$y=\varphi _1 (x) y=\varphi _2 (x)$ Ограниченную замкнутую область $\mathbf { \textit { D } } $, правильную в направлении оси $\mathbf { \textit { Oy } } $, можно описать неравенствами

$D:\left[ \begin{array} { l } a\leqslant x\leqslant b, \newline \varphi _1 (x)\leqslant y\leqslant \varphi _2 (x) \newline \end{array} \right].$

Числа $\mathbf { \textit { a } } $ и $\mathbf { \textit { b } } $ существуют вследствие ограниченности области $\mathbf { \textit { D } } $, функция $\varphi _1 (x)$ образована нижними точками пересечения прямой $\mathbf { \textit { x } } =\mathbf { \textit { x } } _ { 0 } $ при $a<x_0 <b$ с границей области $\mathbf { \textit { D } } $, функция $\varphi _2 (x)$ - верхними точками пересечения этой прямой с границей области $\mathbf { \textit { D } } $.

Аналогичным образом область $\mathbf { \textit { D } } $, ограниченную, замкнутую и правильную в направлении оси $\mathbf { \textit { Oх } } $, можно описать неравенствами

$D:\left[ \begin{array} { l } c\leqslant y\leqslant d, \newline \psi _1 (y)\leqslant x\leqslant \psi _2 (y) \newline \end{array} \right].$

Функция $\psi _1 (y)$ образована левыми точками пересечения прямой $\mathbf { \textit { y } } =\mathbf { \textit { y } } _ { 0 } $ при $c<y_0 <d$ с границей области $\mathbf { \textit { D } } $, функция $\psi _2 (y)$ - правыми точками пересечения этой прямой с границей области $\mathbf { \textit { D } } $.

$x=\psi _2 (y) x=\psi _1 (y)$ Для правильной области { т.е. области, правильной в направлении обеих осей } существуют оба способа представления:

$D:\left[ \begin{array} { l } a\leqslant x\leqslant b, \newline \varphi _1 (x)\leqslant y\leqslant \varphi _2 (x) \newline \end{array} \right]$ и $D:\left[ \begin{array} { l } c\leqslant y\leqslant d, \newline \psi _1 (y)\leqslant x\leqslant \psi _2 (y) \newline \end{array} \right].$

Двукратный { повторный } интеграл

Пусть $\mathbf { \textit { D } } $ - область, простая в направлении оси $\mathbf { \textit { Oy } } $. Рассмотрим выражение $J(D)=\int\limits_a^b { \left( { \int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } }\right)dx } $. Эта конструкция определяется через два обычных определённых интеграла. После интегрирования по $\mathbf { \textit { у } } $ во внутреннем интеграле { переменная $\mathbf { \textit { х } } $ при этом рассматривается как постоянная } и подстановки по $\mathbf { \textit { у } } $ в пределах от $\varphi _1 (x)$ до $\varphi _2 (x)$ получается функция, зависящая только от $\mathbf { \textit { х } } $, которая интегрируется в пределах от $\mathbf { \textit { a } } $ до $\mathbf { \textit { b } } $. В дальнейшем мы будем обычно записывать этот объект без внутренних скобок:

$$ J(D)=\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } . $$

Можно показать, что двукратный интеграл обладает всеми свойствами двойного интеграла:

Свойства линейности и интегрирования неравенств следуют из этих свойств определённого интеграла; интеграл от единичной функции даёт площадь области $\mathbf { \textit { D } } $: $\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { dy } } =\int\limits_a^b { dx\cdot \left. y \right|_ { \varphi _1 (x) } ^ { \varphi _2 (x) } } =\int\limits_a^b { \left[ { \varphi _2 (x)-\varphi _1 (x) }\right]dx } =s(D)$;

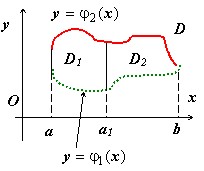
$y=\varphi _1 (x) y=\varphi _2 (x)$ теоремы об оценке и о среднем следуют из перечисленных свойств. Единственное свойство, с которым придётся повозиться - это свойство аддитивности. Мы докажем его в простой, но достаточной для нас форме: если область $\mathbf { \textit { D } } $ разбита на две подобласти $\mathbf { \textit { D } } _ { 1 } $ и $\mathbf { \textit { D } } _ { 2 } $ прямой, параллельной одной из координатных осей, то двукратный интеграл по области $\mathbf { \textit { D } } $ равен сумме интегралов по $\mathbf { \textit { D } } _ { 1 } $ и $\mathbf { \textit { D } } _ { 2 } $: $\mathbf { \textit { J } } (\mathbf { \textit { D } } )=\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 2 } )$.

Первый случай:

прямая $\mathbf { \textit { x } } =\mathbf { \textit { a } } _ { 1 } $ параллельна оси $\mathbf { \textit { Oy } } $. Тогда $J(D)=\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } =\int\limits_a^ { a_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { a_1 } ^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } $ { аддитивность внешнего интеграла } = $\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 2 } )$.

$y=\varphi _2 (x) y=\varphi _2 (x)$

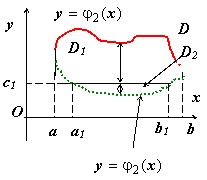
Второй случай:

прямая $\mathbf { \textit { y } } =\mathbf { \textit { c } } _ { 1 } $ параллельна оси $\mathbf { \textit { Oх } } $. Воспользуемся сначала аддитивностью внешнего интеграла: $J(D)=\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } = y=\varphi _1 (x) =\int\limits_a^ { a_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { a_1 } ^ { b_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { b_1 } ^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } =$ { теперь применим свойство аддитивности для внутреннего интеграла в среднем слагаемом } $\textbf { = } \int\limits_a^ { a_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { a_1 } ^ { b_1 } { dx\left[ { \int\limits_ { \varphi _1 (x) } ^ { с_1 } { f(x,y)dy } +\int\limits_ { с_1 } ^ { \varphi _2 (x) } { f(x,y)dy } }\right] } +\int\limits_ { b_1 } ^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } = $ { применяем свойство линейности для внешнего интеграла в среднем слагаемом и перегруппировываем сумму } =$ =\int\limits_a^ { a_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { a_1 } ^ { b_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { с_1 } { f(x,y)dy } } +\int\limits_ { a_1 } ^ { b_1 } { dx\int\limits_ { с_1 } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { b_1 } ^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } =$ $ =\left [ { \int\limits_a^ { a_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } +\int\limits_ { a_1 } ^ { b_1 } { dx\int\limits_ { с_1 } ^ { \varphi _2 (x) } { f(x,y)dy } + } \int\limits_ { b_1 } ^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } }\right ]+ \left [ { \int\limits_ { a_1 } ^ { b_1 } { dx\int\limits_ { \varphi _1 (x) } ^ { с_1 } { f(x,y)dy } } }\right ] $

первая скобка даёт повторный интеграл по $\mathbf { \textit { D } } _ { 1 } $, вторая - по $_ { } \mathbf { \textit { D } } _ { 2 } =\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 2 } )$.

Понятно, что возможны различные случаи взаимного расположения прямых $\mathbf { \textit { y } } =\mathbf { \textit { c } } _ { 1 } $, $\mathbf { \textit { x } } =\mathbf { \textit { a } } _ { 1 } $, $\mathbf { \textit { x } } =\mathbf { \textit { a } } _ { 2 } $ и функций $y=\varphi _1 (x)$, $y=\varphi _2 (x)$, но логика доказательства во всех случаях такая же.

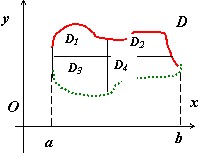
Обобщим доказанное свойство. Пусть прямая разбивает область $\mathbf { \textit { D } } $ на две подобласти $\mathbf { \textit { D } } _ { 1,1 } $ и $\mathbf { \textit { D } } _ { 1,2 } $. Проведём ещё одну прямую, параллельную какой-либо координатной оси. Пусть эта прямая разбивает $\mathbf { \textit { D } } _ { 1,1 } $ на $\mathbf { \textit { D } } _ { 1 } $ и$\mathbf { \textit { D } } _ { 2 } $; $\mathbf { \textit { D } } _ { 1,2 } $ - на $\mathbf { \textit { D } } _ { 3 } $ и $\mathbf { \textit { D } } _ { 4 } $. По доказанному, $\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1,1 } )=\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 2 } )$, $\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1,2 } )=\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 3 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 4 } )$, поэтому $\mathbf { \textit { J } } (\mathbf { \textit { D } } )=\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1,1 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1,2 } )=\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 1 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 2 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 3 } )+\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { 4 } )$. Продолжая рассуждать также, убеждаемся в справедливости следующего утверждения: если область $\mathbf { \textit { D } } $ с помощью прямых, параллельных координатным осям, разбита на подобласти $\mathbf { \textit { D } } _ { 1 } $, $\mathbf { \textit { D } } _ { 2 } , { \ldots } , \mathbf { \textit { D } } _ { n } $, то $J(D)=J(D_1 )+J(D_2 )+\ldots +J(D_n )=\sum\limits_ { i=1 } ^n { J(D_i ) } $.

Теорема о переходе от двойного интеграла к повторному

Пусть $\mathbf { \textit { D } } $ - простая в направлении оси $\mathbf { \textit { Oy } } $ область. Тогда двойной интеграл от непрерывной функции по области $\mathbf { \textit { D } } $ равен повторному интегралу от той же функции по области $\mathbf { \textit { D } } $: $\iint\limits_D { f(x,y)dxdy } =\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } $.

Док-во: Разобьём область $\mathbf { \textit { D } } $ с помощью прямых, параллельных координатным осям, на подобласти $\mathbf { \textit { D } } _ { 1 } $, $\mathbf { \textit { D } } _ { 2 } $, { \ldots } , $\mathbf { \textit { D } } _ { n } $. По доказанному выше, $J(D)=\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } =\sum\limits_ { i=1 } ^n { J(D_i ) } $. К каждому из интегралов $\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { i } )$ применим теорему о среднем: в любой области $\mathbf { \textit { D } } _ { i } $ найдётся точка $\mathbf { \textit { P } } _ { i } $ такая, что $\mathbf { \textit { J } } (\mathbf { \textit { D } } _ { i } )=\mathbf { \textit { f } } (\mathbf { \textit { P } } _ { i } ) \quad \mathbf { \textit { s } } (\mathbf { \textit { D } } _ { i } )$. Следовательно, $J(D)=\sum\limits_ { i=1 } ^n { f(P_i )s(D_i ) } $. В последнем равенстве справа стоит интегральная сумма для двойного интеграла $\iint\limits_D { f(x,y)dxdy } $. Будем мельчить разбиение области так, чтобы $d=\mathop { \max } \limits_ { i=1,2,\ldots ,n } diam(D_i )\to 0$. Вследствие непрерывности функции $\mathbf { \textit { f } } (\mathbf { \textit { x } } $, $\mathbf { \textit { y } } )$ по теореме существования интегральная сумма при этом стремится к двойному интегралу $\iint\limits_D { f(x,y)dxdy } $, т.е. в пределе получим $\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } =\iint\limits_D { f(x,y)dxdy } $, что и требовалось доказать.

Если область $\mathbf { \textit { D } } $ правильная в направлении оси $\mathbf { \textit { Oх } } $, то аналогично доказывается формула $\iint\limits_D { f(x,y)dxdy } =\int\limits_с^d { dy\int\limits_ { \psi _1 (y) } ^ { \psi _2 (y) } { f(x,y)dx } } $. Если $\mathbf { \textit { D } } $ правильна в направлении обеих осей, то для вычисления двойного интеграла можно применять любую из эти формул: $\iint\limits_D { f(x,y)dxdy } =\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { f(x,y)dy } } =\int\limits_с^d { dy\int\limits_ { \psi _1 (y) } ^ { \psi _2 (y) } { f(x,y)dx } } $.

Если область не является правильной, её разбивают на правильные подобласти.