Механические приложения двойного интеграла

Будем считать, что $\mathbf { \textit { D } } $ - неоднородная плоская пластина с поверхностной плотностью материала в точке $P$ равной $\mu (P)$. В механике $\mu (P)$ определяется так. Точка $P$ окружается малой областью $\mathbf { \textit { S } } $, находится масса $\mathbf { \textit { m } } (\mathbf { \textit { S } } )$ и площадь этой области { площадь тоже будем обозначать буквой $\mathbf { \textit { S } } $ } и $\mu (P)=\mathop { \lim } \limits_ { diam(S)\to 0 } \frac { m(S) } { S } $.

Для нахождения массы по заданной плотности мы решим обратную задачу. Разобьём $\mathbf { \textit { D } } $ на малые подобласти $\mathbf { \textit { D } } _ { 1 } $, $\mathbf { \textit { D } } _ { 2 } $,$\mathbf { \textit { D } } _ { 3 } , { \ldots } , \mathbf { \textit { D } } _ { n } $, в каждой из подобластей $\mathbf { \textit { D } } _ { i } $ выберем произвольную точку $\mathbf { \textit { P } } _ { i } $, и, считая что в пределах $\mathbf { \textit { D } } _ { i } $ плотность постоянна и равна $\mu (P_i )$, получим, что масса $\mathbf { \textit { D } } _ { i } $ приближённо есть $\mu (P_i )\cdot s(D_i )$, а масса всей пластины $\sum\limits_ { i=1 } ^n { \mu (P_i )\cdot s(D_i ) } $.

Это интегральная сумма, при уменьшении $d=\mathop { \max } \limits_ { i=1,2,\ldots ,n } diam(D_i )$ точность приближения увеличивается, и в пределе $m(D)=\mathop { \lim } \limits_ { \begin{array} { l } d\to 0 \\ (n\to \infty ) \\ \end{array} } \sum\limits_ { i=1 } ^n { \mu (P_i )\cdot \Delta s(D_i ) } =\iint\limits_D { \mu (P)ds } $.

Аналогично находятся другие параметры пластины:

Координаты центра тяжести

$x_c =\frac { 1 } { m(D) } \iint\limits_D { x\cdot \mu (P)ds } $, $y_c =\frac { 1 } { m(D) } \iint\limits_D { y\cdot \mu (P)ds } $;

Моменты инерции пластины

• $I_x =\iint\limits_D { y^2\cdot \mu (P)ds } $ { относительно оси $\mathbf { \textit { Ox } } $ } ,
• $I_y =\iint\limits_D { x^2\cdot \mu (P)ds } $ { относительно оси $\mathbf { \textit { Oy } } $ } ,
• $I_O =\iint\limits_D { (x^2+y^2)\cdot \mu (P)ds } =I_x +I_y $ { относительно начала координат } .

Пластина расположена в области (R) и ее плотность в точке ( { \left( { x,y }\right) } ) равна ( { \rho \left( { x,y }\right) } ).

Масса пластины

(m = \large\iint\limits_R\normalsize { \rho \left( { x,y }\right)dA } )

Статические моменты пластины

Момент пластины относительно оси (Ox) определяется формулой

( { M_x } = \large\iint\limits_R\normalsize { y\rho \left( { x,y }\right)dA } )

Аналогично, момент пластины относительно оси (Oy) выражается в виде

( { M_y } = \large\iint\limits_R\normalsize { x\rho \left( { x,y }\right)dA } )

Координаты центра масс пластины

• (\bar x = \large\frac { { { M_y } } } { m } \normalsize = \large\frac { 1 } { m } \normalsize \large\iint\limits_R\normalsize { x\rho \left( { x,y }\right)dA } = \large\frac { { \iint\limits_R { x\rho \left( { x,y }\right)dA } } } { { \iint\limits_R { \rho \left( { x,y }\right)dA } } } \normalsize,\;)
• (\bar y = \large\frac { { { M_x } } } { m } \normalsize = \large\frac { 1 } { m } \normalsize \large\iint\limits_R\normalsize { y\rho \left( { x,y }\right)dA } = \large\frac { { \iint\limits_R { y\rho \left( { x,y }\right)dA } } } { { \iint\limits_R { \rho \left( { x,y }\right)dA } } } \normalsize ).

Заряд пластины

(Q = \large\iint\limits_R\normalsize { \sigma \left( { x,y }\right)dA } ),

где электрический заряд распределен по области (R) и его плотность в точке ( { \left( { x,y }\right) } ) равна ( { \sigma \left( { x,y }\right) } ).

Среднее значение функции

(\mu = \large\frac { 1 } { S } \iint\limits_R\normalsize { f\left( { x,y }\right)dA } ,\;) где (S = \large\iint\limits_R\normalsize { dA } ).

Пример 1

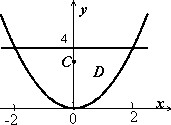
Найти параметры неоднородной плоской пластины, ограниченной кривыми

$D:\left[{ \begin{array} { l } y=x^2, \\ y=4; \\ \end{array} }\right.$ если плотность $\mu (x,y)=y+1$.

Решение:

$m(D)=\iint\limits_D { (y+1)dxdy } =2\int\limits_0^2 { dx } \int\limits_ { x^2 } ^4 { (y+1)dy } =2\int\limits_0^2 { \left. { \left( { y^2/2+y }\right) }\right|_ { x^2 } ^4 dx } =$ $ =2\int\limits_0^2 { \left( { 12-x^4/2-x^2 }\right)dx } =2\left. { \left( { 12x-x^5/10-x^3/3 }\right) }\right|_0^2 =2\left( { 24-\frac { 16 } { 5 } -\frac { 8 } { 3 } }\right)=\frac { 544 } { 15 } . $ $ x_c =\frac { 1 } { m(D) } \iint\limits_D { x(y+1)dx } dy=\frac { 15 } { 544 } \int\limits_ { -2 } ^2 { dx } \int\limits_ { x^2 } ^4 { x(y+1)dy } =\frac { 15 } { 544 } \int\limits_ { -2 } ^2 { x\left. { \left( { y^2/2+y }\right) }\right|_ { x^2 } ^4 dx } = $ $=\frac { 15 } { 544 } \int\limits_ { -2 } ^2 { \left( { 12x-x^5/2-x^3 }\right)dx } = \quad =\frac { 1 } { 544 } \left. { \left( { 6x^2-x^6/10-x^4/4 }\right) }\right|_ { -2 } ^2 =0$ { что и следовало ожидать, так как область и плотность симметричны относительно оси Оу). $ \begin{array} { l } y_c =\frac { 1 } { m(D) } \iint\limits_D { y(y+1)dx } dy=\frac { 15 } { 544 } \int\limits_ { -2 } ^2 { dx } \int\limits_ { x^2 } ^4 { y(y+1)dy } =\frac { 15 } { 272 } \int\limits_0^2 { \left. { \left( { y^3/3+y^2/2 }\right) }\right|_ { x^2 } ^4 dx } = \\ =\frac { 15 } { 272 } \int\limits_0^2 { \left( { 64/3+8-x^6/3-x^4/2 }\right)dx } =\frac { 15 } { 272 } \left. { \left( { 88x/3-x^7/21-x^5/10 }\right) }\right|_0^2 =\frac { 15 } { 272 } \left( { \frac { 176 } { 3 } -\frac { 128 } { 21 } -\frac { 16 } { 5 } }\right)=\frac { 15 } { 272 } \cdot \frac { 1728 } { 35 } \approx 2,72. \\ \end{array} $ $ I_x =\iint\limits_D { y^2(y+1)dx } dy=2\int\limits_0^2 { dx } \int\limits_ { x^2 } ^4 { y^2(y+1)dy } =2\int\limits_0^2 { \left. { \left( { y^4/4+y^3/3 }\right) }\right|_ { x^2 } ^4 dx } =2\int\limits_0^2 { \left( { \frac { 256 } { 3 } -\frac { x^8 } { 4 } -\frac { x^6 } { 3 } }\right)dx } = $ $ =2\left. { \left( { \frac { 256 } { 3 } x-\frac { x^9 } { 36 } -\frac { x^7 } { 21 } }\right) }\right|_0^2 \approx 300,7. $ $ I_y =\iint\limits_D { x^2(y+1)dx } dy=2\int\limits_0^2 { x^2dx } \int\limits_ { x^2 } ^4 { (y+1)dy } =2\int\limits_0^2 { x^2\left. { \left( { y^2/2+y }\right) }\right|_ { x^2 } ^4 dx } =2\int\limits_0^2 { x^2\left( { 12-\frac { x^4 } { 2 } -x^2 }\right)dx } = $ $ =2\left. { \left( { 4x^3-\frac { x^7 } { 14 } -\frac { x^5 } { 5 } }\right) }\right|_0^2 \approx 32,9. \quad I_O =\iint\limits_D { \left( { x^2+y^2 }\right)(y+1)dx } dy=I_x +I_y \approx 333,6. $

Пример 2

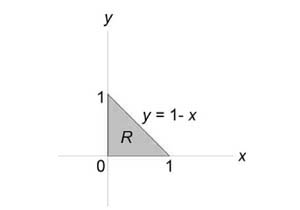
Вычислить моменты инерции треугольника, ограниченного прямыми (x + y = 1,) (x = 0,) (y = 0) и имеющего плотность $\rho \left( { x,y }\right) = xy.$

Решение:

Найдем момент инерции пластины относительно оси (Ox:) $ { { I_x } = \iint\limits_R { { y^2 } \rho \left( { x,y }\right)dxdy } } = { \int\limits_0^1 { \left[ { \int\limits_0^ { 1 - x } { { y^2 } xydy } }\right]dx } } = { \int\limits_0^1 { \left[ { \int\limits_0^ { 1 - x } { { y^3 } dy } }\right]xdx } } = { \int\limits_0^1 { \left[ { \left. { \left( { \frac { { { y^4 } } } { 4 } }\right) }\right|_0^ { 1 - x } }\right]xdx } } = \\ = { \frac { 1 } { 4 } \int\limits_0^1 { { { \left( { 1 - x }\right) } ^4 } xdx } } = { \frac { 1 } { 4 } \int\limits_0^1 { \left( { 1 - 4x + 6 { x^2 } - 4 { x^3 } + { x^4 } }\right)xdx } } = \\ = { \frac { 1 } { 4 } \int\limits_0^1 { \left( { x - 4 { x^2 } + 6 { x^3 } - 4 { x^4 } + { x^5 } }\right)dx } } = { \frac { 1 } { 4 } \left. { \left( { \frac { { { x^2 } } } { 2 } - \frac { { 4 { x^3 } } } { 3 } + \frac { { 6 { x^4 } } } { 4 } - \frac { { 4 { x^5 } } } { 5 } + \frac { { { x^6 } } } { 6 } }\right) }\right|_0^1 } = { \frac { 1 } { 4 } \left( { \frac { 1 } { 2 } - \frac { 4 } { 3 } + \frac { 3 } { 2 } - \frac { 4 } { 5 } + \frac { 1 } { 6 } }\right) } = { \frac { { 49 } } { { 120 } } . } $

Аналогично вычислим момент инерции относительно оси (Oy:) $ { { I_y } = \iint\limits_R { { x^2 } \rho \left( { x,y }\right)dxdy } } = { \int\limits_0^1 { \left[ { \int\limits_0^ { 1 - x } { { x^2 } xydy } }\right]dx } } = { \int\limits_0^1 { \left[ { \int\limits_0^ { 1 - x } { ydy } }\right] { x^3 } dx } } = { \int\limits_0^1 { \left[ { \left. { \left( { \frac { { { y^2 } } } { 2 } }\right) }\right|_0^ { 1 - x } }\right] { x^3 } dx } } = { \frac { 1 } { 2 } \int\limits_0^1 { { { \left( { 1 - x }\right) } ^2 } { x^3 } dx } } = \\ = { \frac { 1 } { 2 } \int\limits_0^1 { \left( { 1 - 2x + { x^2 } }\right) { x^3 } dx } } = { \frac { 1 } { 2 } \int\limits_0^1 { \left( { { x^3 } - 2 { x^4 } + { x^5 } }\right)dx } } = { \frac { 1 } { 2 } \left. { \left( { \frac { { { x^4 } } } { 4 } - \frac { { 2 { x^5 } } } { 5 } + \frac { { { x^6 } } } { 6 } }\right) }\right|_0^1 } = { \frac { 1 } { 2 } \left( { \frac { 1 } { 4 } - \frac { 2 } { 5 } + \frac { 1 } { 6 } }\right) } = { \frac { 1 } { { 120 } } . } $

Пример 3

Электрический заряд распределен по площади диска ( { x^2 } + { y^2 } = 1) таким образом, что его поверхностная плотность равна $\sigma \left( { x,y }\right) = 1 + { x^2 } + { y^2 } \;\left( { \text { Кл/м } ^2 }\right)$ Вычислить полный заряд диска.

Решение:

В полярных координатах область, занятая диском, описывается множеством (\left[{ \left( { r,\theta }\right)|\;0 \le r \le 1,0 \le \theta \le 2\pi }\right].)

Полный заряд будет равен $ { Q = \iint\limits_R { \sigma \left( { x,y }\right)dxdy } } = { \int\limits_0^ { 2\pi } { \left[ { \int\limits_0^1 { \left( { 1 + { r^2 } { { \cos } ^2 } \theta + { r^2 } { \sin^2 } \theta }\right)rdr } }\right]d\theta } } = { \int\limits_0^ { 2\pi } { d\theta } \int\limits_0^1 { \left( { 1 + { r^2 } }\right)rdr } } = { 2\pi \int\limits_0^1 { \left( { r + { r^3 } }\right)dr } } = \\ = { 2\pi \left. { \left( { \frac { { { r^2 } } } { 2 } + \frac { { { r^4 } } } { 4 } }\right) }\right|_0^1 } = { 2\pi \left( { \frac { 1 } { 2 } + \frac { 1 } { 4 } }\right) } = { \frac { { 3\pi } } { 2 } \;\left( { \text { Кл } }\right). } $